Can an Object with Constant Speed Be Accelerating?

An interesting question is whether an object with a constant speed can still be accelerating, and intuitively the answer would be “no”: acceleration means the object is speeding up or slowing down, right? Apparently, this is not the case. It actually is possible to have a constant speed while still having an acceleration. In this post, we will look at how this is possible. Hint: circular motion!

A schematic of circulator motion: an object is drawn describing a circle of radius r. An arrow is drawn tangential to the object’s current point on the circle labeled with vector v. — Circular Motion

Let’s imagine an object traveling with constant speed $v$ on a perfectly circular path with radius $r$ . We can describe the position of the object as a function of time: $\vec{R}(t)$ . This vector has an angle of $\theta(t)$ with the X-axis (the angle is a function of time, as the object is moving around the origin) and can be decomposed into its X- and Y-components.

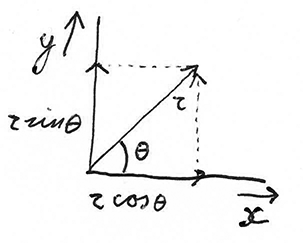
A schematic of a point at a distance of radius r from the origin, with a line from the origin to the point’s position at an angle of theta from the horizontal. The vertical component of the point’s position is labeled r sin(theta). The horizontal component of the point’s position is labeled r cos(theta). — $\vec{R}$ can be expressed in terms of Sine and Cosine of the angle.

We’ll express the position-vector as $\vec{R}(t) = r \left(\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j} \right)$ . Here, $\vec{i}$ is the unit vector in the +X direction, and $\vec{j}$ is the unit vector in the +y direction.

We have:

\begin{aligned} \vec{v}(t) &= \frac{\delta \vec{R}(t)}{\delta t} \\ &= r \left(-\sin(\theta(t)) \frac{\delta \theta(t)}{\delta t} \vec{i} + \cos(\theta(t)) \frac{\delta \theta(t)}{\delta t} \vec{j} \right) \\ &= r \left(-\sin(\theta(t)) \omega \vec{i} + \cos(\theta(t)) \omega \vec{j} \right) \\ &= r \omega \left(-\sin(\theta(t)) \vec{i} + \cos(\theta(t)) \vec{j} \right) \end{aligned}

Note that the change in angle $\frac{\delta \theta(t)}{\delta t} = \omega$ with $\omega$ the angular velocity.

Using this, we find the acceleration:

\begin{aligned} \vec{a}(t) &= \frac{\delta \vec{v}(t)}{\delta t} \\ &= r \omega \left(-\cos(\theta(t)) \frac{\delta \theta(t)}{\delta t} \vec{i} - \sin(\theta(t)) \frac{\delta \theta(t)}{\delta t} \vec{j} \right) \\ &= r \omega \left(-\cos(\theta(t)) \omega \vec{i} - \sin(\theta(t)) \omega \vec{j} \right) \\ &= -r \omega^2 \left(\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j} \right) \end{aligned}

It is interesting to note that, rearranging some terms, we get:

\begin{aligned} \vec{a}(t) &= -\omega^2 r \left(\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j} \right) \\ &= -\omega^2 R(t) \end{aligned}

In other words, the acceleration vector has opposite direction to the position vector and has a magnitude of $\omega^2$ times the radius.

In the case of a circular motion, the angular velocity $\omega$ is equal to $\frac{v}{r}$ . With this in mind, all that remains is finding the magnitude of $\vec{a}(t)$ :

\begin{aligned} a(t) & = |-\omega^2 R(t)| \\ &= |-\omega^2| |R(t)| \\ &= |-\left(\frac{v}{r}\right)^2| |r \left(\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j} \right) \\ &= \frac{v^2}{r^2} r |\left(\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j} \right) | \\ &= \frac{v^2}{r} \end{aligned}

For the last step, note that $\cos(\theta(t)) \vec{i} + \sin(\theta(t)) \vec{j}$ describes the unit circle on the X- and Y-axes, and thus this expression has magnitude 1. So, an object with a constant speed can actually be accelerating! We see this in practice in many orbits. For example, the Moon is constantly pulled towards the Earth by gravity, and so is constantly accelerating towards the Earth, but the orbit of the Moon around the Earth describes a roughly circular motion with constant speed!

We already found that the acceleration has a direction opposite to the position vector (when the center of the circle is chosen as the center of the coordinate system). Let’s now find the angle between the acceleration and velocity vectors using the definition of the in-product of vectors.

\vec{a}(t) \cdot \vec{v}(t) = |a(t)| \cdot |v(t)| \cdot \cos(\phi)

With $\phi$ the angle between vectors $\vec{a}(t)$ and $\vec{v}(t)$ . By using the definition of the in-product in that $(a \vec{i} + b \vec{j}) \cdot (c \vec{i} + d \vec{j}) = ac + bd$ , we get:

\begin{aligned} \vec{a}(t) \cdot \vec{v}(t) &= |a(t)| \cdot |v(t)| \cdot \cos(\phi) \\ &= r^2 w^3 \cos(\theta(t)) \cdot \sin(\theta(t)) - r^2 w^3 \sin(\theta(t)) \cdot \cos(\theta(t)) \\ &= -r^2 w^3 \left(-\cos(\theta(t)\right) \sin(\theta(t)) + \cos(\theta(t)) \sin(\theta(t)) \\ &= 0 \end{aligned}

Then:

\begin{aligned} \cos(\phi) &= \frac{\vec{a}(t) \cdot \vec{v}(t)}{|a(t)| \cdot |v(t)|} \\ &= \frac{0}{|a(t)| \cdot |v(t)|} \\ &= 0 \\ \phi &= cos^{-1}(0) = 90 ^\circ \end{aligned}

So, the acceleration is perpendicular to the velocity. This is called radial acceleration. In general, acceleration can be decomposed in radial and tangential parts. The radial part is perpendicular to the velocity, and the tangential part is in the same or opposite direction as the velocity. The radial part causes the velocity to change direction, and the tangential part causes the velocity to change in magnitude!

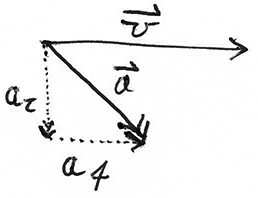
A schematic of an object with a velocity vector and an acceleration vector acting on it. The acceleration vector is decompose into two orthogonal vectors: a_r (perpendicular to the velocity) and a_t (parallel to the velocity). — $\vec{a}$ can be decomposed into $a_r$ and $a_t$ .