The Kessel Run in Less than Twelve Parsecs

The millennium falcon seen just off-angle from head-on. — You’ve never heard of the Millennium Falcon?… It’s the ship that made the Kessel Run in less than twelve parsecs. – Han Solo

If you’ve seen Star Wars: A New Hope, you’ll have heard the above quote. People often think Solo refers to his ship’s speed when he says this, but that is not the case. A parsec is a unit of length, not of time! In fact, it is defined as the distance from the sun to an astronomical object such that the parallax angle (the angle between lines from the Earth and the Sun to that object) is one second of arc. Parallax One parsec is the distance from the Sun to a nearby astronomical object that has a parallax angle of 1 second of arc.

A schematic drawing of the angle of 1 arcsec and the distances 1 parsec and 1
au. A line is drawn between a star and a body labeled with a distance of 1
parsec. An object is orbiting the star labeled with a distance of 1 au. From
two opposite sides of the orbit lines are drawn to the distant object. The
lines from the orbiting body and the sun to the distant object are marked as
having an angle of 1 arcsec. — One parsec is the distance from the Sun to a nearby astronomical object that has a parallax angle of 1 second of arc.

Using this information, we will calculate the length of a parsec in meters.

When you are in motion, for example on a train, parallax is the effect where objects close to you (houses next to the track) appear to move faster than objects farther away (the treeline in the distance). The same effect occurs on an astronomical scale. As the Earth orbits around the Sun, astronomical objects such as stars that are close to us appear to move faster than objects farther away. Because the Earth’s path is roughly a circle, the closer stars appear to wobble against the background. (We call the “background” all objects far enough away such that we can treat them as static for our intentions.)

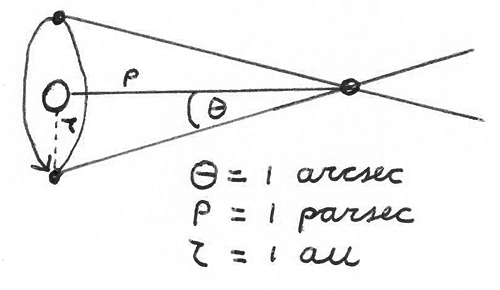
If you draw a line from the Earth to a near star and another line from the Sun to the same star, the lines are at an angle of $\theta$ . When the lines from the Earth and the Sun to that star have an angle of $\theta = 1 \text{ arcsec}$ , the length of the line from the Sun to that star is one parsec. One second of arc is equal to a sixtieth of a minute of arc, which is a sixtieth of a degree: $\theta = 1 \text{ arcsec} = 1/60/60 = 1/3600 ^\circ$ .

As a result, the situation can be described by the following triangle. The distance from the Earth to the Sun is, on average, one astronomical unit (au), which is exactly 149,597,870,700 meters. We have:

"posts/2014-the-kessel-run-in-less-than-twelve-parsecs/parsec-triangle-bw.png"

\begin{aligned} \tan\left(\theta\right) &= \frac{1 \text{ au}}{p} \\ p &= \frac{1 \text{ au}}{\tan\left(\theta\right)} \end{aligned}

Now we just plug in the values to get $p = \frac{149,597,870,700 \text{ m}}{\tan\left(1/3600 ^\circ\right)} \approx 3.086 \cdot 10^{16} \text{ meters}$ . To put this number in perspective, a light particle traveling through a vacuum would need 3.3 years to cover this distance! Man, those spaceships in Star Wars get quite some mileage…