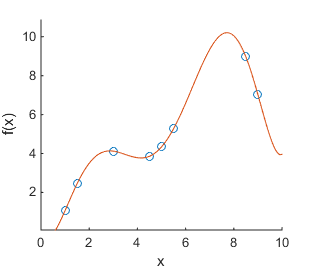
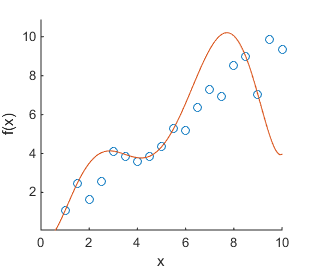
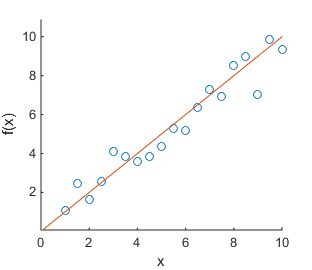
Finding models that predict or explain relationships in data is a big focus in information science. Such models often have many parameters that can be tuned, and in practice we only have limited data to tune the parameters with. If we make measurements of a function f(x) at different values of x, we might find data like in Figure (a) below. If we now fit a polynomial curve to all known data points, we might find the model that is depicted in Figure (b). This model appears to explain the data perfectly: all data points are covered. However, such a model does not give any additional insight into the relationship between x and f(x). Indeed; if we make more measurements, we find the data in Figure (c). Now the model we found in (b) appears to not fit the data well at all. In fact, the function used to generate the data is f(x) = x + \epsilon with \epsilon Gaussian noise. The linear model f'(x) = x depicted in Figure (d) is the most suitable model to explain the found data and to make predictions of future data.

The overly complex model found in (b) is said to have overfitted. A model that has been overfitted fits the known data extremely well, but it is not suited for generalization to unseen data. Because of this, it is important to have some estimate of a model’s ability to be generalized to unseen data. This is where training, testing, and development sets come in. The full set of collected data is split into these separate sets.

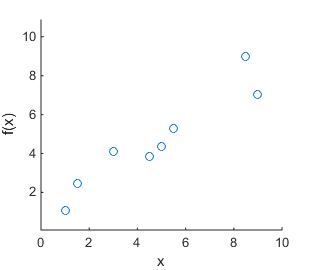
Training Set

The training set is the part of all the collected data that is used to tune a model’s parameters. Generally, this set comprises 50-80% of all data. To increase the probability that a model is generalizable the model’s parameters must be tuned with as much data as possible. So, the training set must be as large as possible, while still allowing for large enough testing and development sets.

Testing Set

The testing set is used to test the generalizability of a fully trained model by testing its ability to predict relationships in unseen data. Once a model is put to use in the real world, it will not have seen any of the data before it has to make a prediction. So, it is important that none of the data points in the testing set have been used to tune any of the model’s parameters, otherwise we do not get a fair estimate of the model’s generalizability. The testing set often comprises 10-25% of all data. The larger the testing set, the more accurate the estimate of generalizability will be.

Development / Validation Set

The development set is closely related to the testing set, but there is a subtle difference between the two. When searching for models that predict relationships in data, you generally try a multitude of models. In addition, you often need to tune model hyper-parameters such as learning rate or parameter regularization. To evaluate and compare these choices, you would train models on the training set and evaluate their ability to be generalized on unseen data. However, (and here comes the subtle part,) if one uses the testing set to evaluate generalizability of models against each other, they are actually tuning the hyper-parameters and model choices to data that should be left completely unseen in order to be able to make a confident statement about the generalizability of a specific model. If that person then uses the testing set to assess the generalizability of the chosen model, they would get an underestimate of the true test error. As such, by using a development set of unseen data to evaluate models against each other, the testing set of unseen data can still be used as an estimate of generalizability of a specific model. The development set often has the same size as the testing set; 10-25% of all data.

Keep in mind that after evaluating the chosen model on the test set, you should not tune the model’s parameters any further.