One of the most common logical inferences uses logical implication. For example, you know that if it rains then the grass will be wet. If you look outside and see that it rains, you do not have to look at the grass to know that it is wet. This inference is called modus ponens: if A implies B and A is true, then B is true. Formally, the implication can be written as:
Introduction to Artificial Neural Networks
An artificial neural network (ANN) is a type of machine learning model. It is made up of a number of simple parts called units, or neurons. By combining a large amount of these simple units, ANNs can solve real-world problems. For example, the main network that was used in my bachelor thesis research consisted of over 12,000 units. The name artificial neural network is slightly misleading: they’re mostly related to biological neural networks through the fact that both artificial and natural neural networks are made up of simple parts. Other than that they’re quite unrelated.
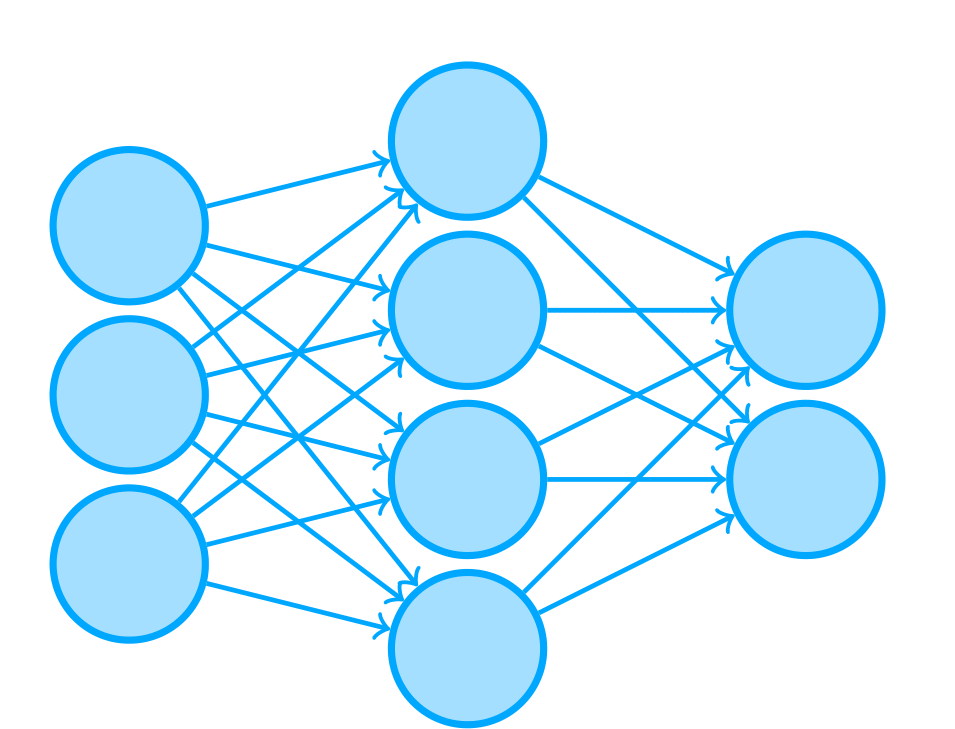
A simple ANN
Decreasing Information
During the training of several neural networks for my bachelor’s thesis (more on that later, maybe!) I noticed something fun. The used networks’ weights (in this case classification function parameters) are initialized with numbers drawn from the standard normal distribution, meaning the initial network state is random. Such randomness by its very nature has no actual structure, and thus has high entropy. This means that compressing the information to save it to disk is less effective than on other, more structured, information. Initially, saving one such network’s weights required approximately 19.5MB of disk space.
Rocket Fuel Requirements Revisited
In a previous post we looked at the fuel requirements for rockets to reach escape velocity. We calculated the fuel requirements using the rocket equation. This equation takes into account the conservation of momentum. However, momentum is not the only property influencing the velocity of the rocket during a launch.
Rockets expel their fuel over time. During this time, the rocket is pulled back due to gravity. Only if a rocket could instantaneously expel all of its fuel, and when ignoring atmospheric drag, the escape velocity would be reached instantaneously and the equation would hold.
Taking the burn-time and gravity into account yields a difficult differential equation. We can implement that equation in a computer program to simulate the launch.
The equation is of the following form:
Black Holes
A black hole is an object from which nothing, including light, is able to escape. As nothing can go faster than light, this can be more formally defined as an object for which the escape velocity is greater than the speed of light. In my post about escape velocity we found an equation relating the velocity required to escape from the gravitational pull of an object and that object’s mass.
Escape Velocity (And: How Much Fuel Do Rockets Need?)
During the launch of a rocket, the Earth’s gravitational field is pulling the rocket back. The rocket needs a certain speed to be able to escape from the Earth’s gravitational field, such that it won’t fall back to Earth nor get into an orbit around it. Escape velocity is the speed a rocket requires to be able to escape from a body without having to burn more fuel later during the maneuver. For a body as massive as Earth, the required velocity is relatively high, and this is why rockets literally need tonnes of fuel.
In this post, by making a few simplifications and using the rocket equation that we found earlier, we will derive an equation to calculate the amount of propellant needed to escape from Earth.
The Rocket Equation
Rockets in space, like all other objects, have to accelerate to change velocity. But space is a vacuum, so there is nothing to push against to create force. Instead, rockets accelerate by using the conservation of momentum. The momentum of an object is equal to the object’s mass multiplied by the object’s velocity: \vec{p} = m \vec{v}. In a closed system, the total momentum remains constant: \vec{p}_{0} = \vec{p}_{t}.
Shorts: Vertical Travel Distance of Bouncing Objects
If a ball is dropped from a height of 10 meters, and on each bounce it reaches a maximal height of 0.75 times the previous height, then what is the total distance traveled? If we use h_i as the maximal height reached on bounce i, h_0 as the initial height, and $latex b $ as the factor of the maximal height achieved relative to the previous bounce, we have h_i = b h_{i-1}. Then, the total distance traveled is:
Can an Object with Constant Speed Be Accelerating?
An interesting question is whether an object with a constant speed can still be accelerating, and intuitively the answer would be “no”: acceleration means the object is speeding up or slowing down, right? Apparently, this is not the case. It actually is possible to have a constant speed while still having an acceleration. In this post, we will look at how this is possible. Hint: circular motion!
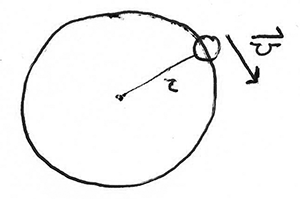
Circular Motion
Relative Velocity (Or: The Velocity-Addition Formula)
With the knowledge that the speed of light is constant and the same for every reference frame, and that no object can travel at the speed of light or faster than the speed of light in any reference frame, we ask ourselves the question: what happens when two spaceships leave from a space station in opposite directions and both reach a constant speed of 0.95c (with c the speed of light) relative to that space station? In the space station’s reference frame, the two ships travel at 2 \cdot 0.95c = 1.9c relative to each other. This doesn’t violate relativity, as neither spaceship is actually going at or faster than the speed of light. But, ignoring the effects of relativity, in the reference frame of either spaceship, the other ship would appear to travel at 1.9c. This would violate relativity!